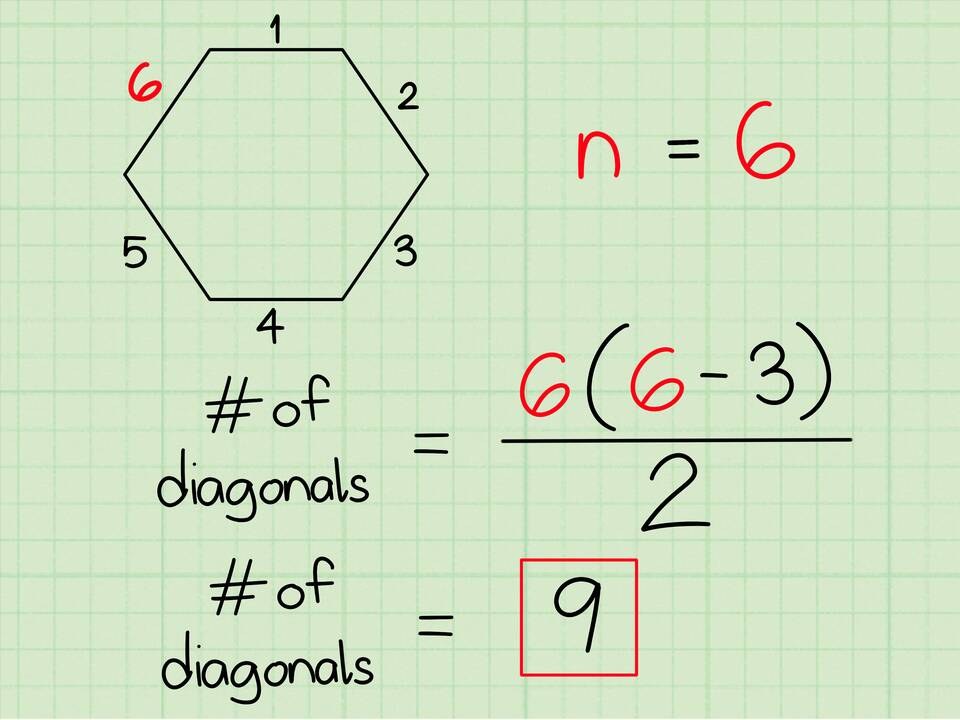В математике и геометрии понятие "выпуклого" может относиться к различным объектам. Рассмотрим методы вычисления суммы для разных типов выпуклых фигур и множеств.
Содержание
Основные понятия выпуклости
- Выпуклая фигура - геометрическая фигура, где отрезок, соединяющий любые две точки, полностью принадлежит фигуре
- Выпуклое множество - множество точек в пространстве, обладающее свойством выпуклости
- Выпуклая функция - функция, график которой лежит ниже хорды между любыми двумя точками
Вычисление суммы выпуклых фигур
| Тип фигуры | Метод нахождения суммы |
| Выпуклый многоугольник | Сумма внутренних углов = (n-2) × 180°, где n - количество сторон |
| Выпуклый многогранник | Сумма углов при вершинах = 360° × (V - 2), где V - количество вершин |
Сумма выпуклых множеств
Алгебраическая сумма двух выпуклых множеств A и B определяется как:
- A + B = {a + b | a ∈ A, b ∈ B}
- Результатом суммы будет новое выпуклое множество
- Для выпуклых оболочек: conv(A) + conv(B) = conv(A + B)
Выпуклые комбинации
- Выпуклая комбинация точек x₁, x₂, ..., xₙ - это выражение вида: Σλᵢxᵢ
- Где λᵢ ≥ 0 и Σλᵢ = 1
- Сумма выпуклых комбинаций сохраняет свойство выпуклости
Примеры расчетов
Сумма углов выпуклого пятиугольника
- Количество сторон n = 5
- Сумма углов = (5-2) × 180° = 540°
Сумма выпуклых множеств
| Множество A | Множество B | A + B |
| [0,1] | [2,3] | [2,4] |
Применение в математическом анализе
- Теорема Каратеодори: любая точка выпуклой оболочки может быть представлена как выпуклая комбинация не более n+1 точек
- Выпуклые оптимизации - нахождение минимума выпуклых функций
- Геометрические вычисления в компьютерной графике
Проверка выпуклости
- Для многоугольника: все внутренние углы меньше 180°
- Для функции: вторая производная неотрицательна на интервале
- Для множества: проверка по определению через отрезки между точками
Заключение
Нахождение суммы выпуклых объектов требует понимания их основных свойств и применения соответствующих математических методов. В зависимости от типа выпуклого объекта (фигура, множество, функция) применяются различные подходы к вычислению характеристик и операций сложения.