Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны. В 8 классе изучаются основные свойства параллелограмма, включая свойства его углов.
Содержание
Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны. В 8 классе изучаются основные свойства параллелограмма, включая свойства его углов.
Основная теорема о сумме углов параллелограмма
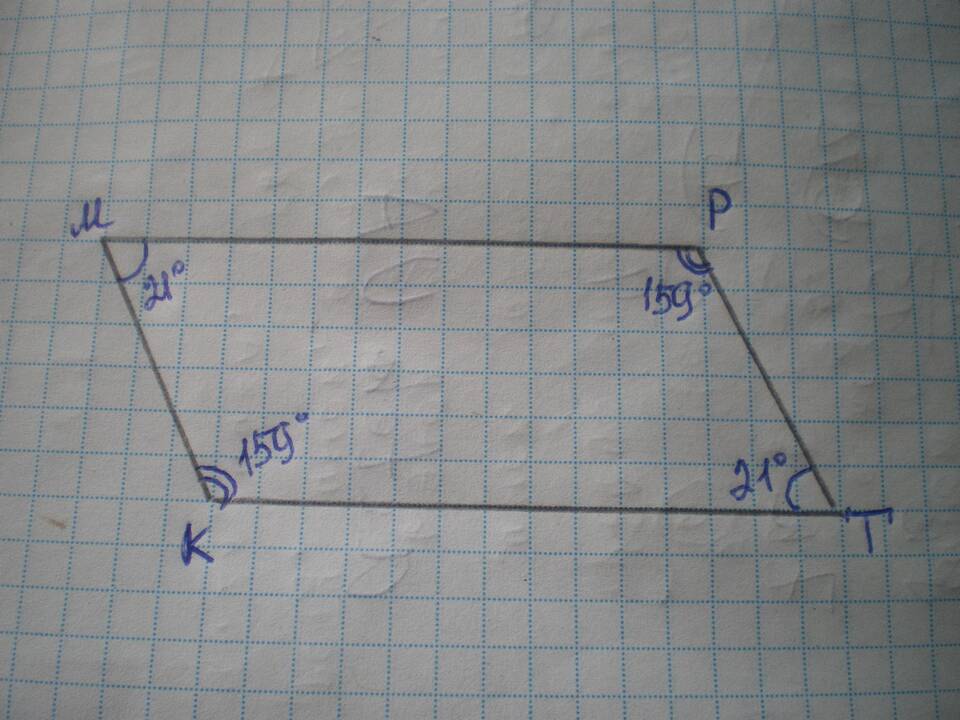
Сумма всех внутренних углов любого параллелограмма равна 360°. Это свойство вытекает из общей теоремы о сумме углов выпуклого четырехугольника.
Доказательство теоремы
- Проведем в параллелограмме ABCD диагональ AC
- Диагональ разбивает параллелограмм на два равных треугольника: ABC и ADC
- Сумма углов каждого треугольника равна 180°
- Следовательно, сумма углов параллелограмма: 180° × 2 = 360°
Свойства углов параллелограмма
| Свойство | Описание |
| Противоположные углы | Равны между собой (∠A = ∠C, ∠B = ∠D) |
| Соседние углы | Дают в сумме 180° (∠A + ∠B = 180°) |
| Сумма всех углов | Всегда равна 360° |
Пример решения задачи
В параллелограмме ABCD угол A равен 65°. Найдите остальные углы.
- ∠C = ∠A = 65° (противоположные углы равны)
- ∠B = 180° - 65° = 115° (соседние углы в сумме дают 180°)
- ∠D = ∠B = 115° (противоположные углы равны)
- Проверка: 65° + 115° + 65° + 115° = 360°
Важные следствия
- Если один угол параллелограмма прямой, то все углы прямые (прямоугольник)
- Биссектрисы соседних углов перпендикулярны друг другу
- Высота параллелограмма образует прямоугольный треугольник
Практическое применение
Знание свойств углов параллелограмма позволяет решать различные геометрические задачи:
- Нахождение неизвестных углов
- Доказательство равенства треугольников
- Решение задач на построение
- Вычисление площадей фигур
Сумма углов параллелограмма, равная 360°, является фундаментальным свойством этой геометрической фигуры, которое широко применяется в решении задач школьного курса геометрии.
